编译表达式

In the middle of the journey of our life I found myself within a dark woods where the straight way was lost.

Dante Alighieri, Inferno

This chapter is exciting for not one, not two, but three reasons. First, it provides the final segment of our VM’s execution pipeline. Once in place, we can plumb the user’s source code from scanning all the way through to executing it.

Second, we get to write an actual, honest-to-God compiler. It parses source code and outputs a low-level series of binary instructions. Sure, it’s bytecode and not some chip’s native instruction set, but it’s way closer to the metal than jlox was. We’re about to be real language hackers.

Third and finally, I get to show you one of my absolute favorite algorithms: Vaughan Pratt’s “top-down operator precedence parsing”. It’s the most elegant way I know to parse expressions. It gracefully handles prefix operators, postfix, infix, mixfix, any kind of -fix you got. It deals with precedence and associativity without breaking a sweat. I love it.

As usual, before we get to the fun stuff, we’ve got some preliminaries to work through. You have to eat your vegetables before you get dessert. First, let’s ditch that temporary scaffolding we wrote for testing the scanner and replace it with something more useful.

InterpretResult interpret(const char* source) {

  Chunk chunk;
  initChunk(&chunk);

  if (!compile(source, &chunk)) {
    freeChunk(&chunk);
    return INTERPRET_COMPILE_ERROR;
  }

  vm.chunk = &chunk;
  vm.ip = vm.chunk->code;

  InterpretResult result = run();

  freeChunk(&chunk);
  return result;

}

We create a new empty chunk and pass it over to the compiler. The compiler will take the user’s program and fill up the chunk with bytecode. At least, that’s what it will do if the program doesn’t have any compile errors. If it does encounter an error, compile() returns false and we discard the unusable chunk.

Otherwise, we send the completed chunk over to the VM to be executed. When the VM finishes, we free the chunk and we’re done. As you can see, the signature to compile() is different now.

#define clox_compiler_h

#include "vm.h"

bool compile(const char* source, Chunk* chunk);

#endif

We pass in the chunk where the compiler will write the code, and then compile() returns whether or not compilation succeeded. We make the same change to the signature in the implementation.

#include "scanner.h"

bool compile(const char* source, Chunk* chunk) {

  initScanner(source);

That call to initScanner() is the only line that survives this chapter. Rip out the temporary code we wrote to test the scanner and replace it with these three lines:

  initScanner(source);

  advance();
  expression();
  consume(TOKEN_EOF, "Expect end of expression.");

}

The call to advance() “primes the pump” on the scanner. We’ll see what it does soon. Then we parse a single expression. We aren’t going to do statements yet, so that’s the only subset of the grammar we support. We’ll revisit this when we add statements in a few chapters. After we compile the expression, we should be at the end of the source code, so we check for the sentinel EOF token.

We’re going to spend the rest of the chapter making this function work, especially that little expression() call. Normally, we’d dive right into that function definition and work our way through the implementation from top to bottom.

This chapter is different. Pratt’s parsing technique is remarkably simple once you have it all loaded in your head, but it’s a little tricky to break into bite-sized pieces. It’s recursive, of course, which is part of the problem. But it also relies on a big table of data. As we build up the algorithm, that table grows additional columns.

I don’t want to revisit 40-something lines of code each time we extend the table. So we’re going to work our way into the core of the parser from the outside and cover all of the surrounding bits before we get to the juicy center. This will require a little more patience and mental scratch space than most chapters, but it’s the best I could do.

17 . 1Single-Pass Compilation

A compiler has roughly two jobs. It parses the user’s source code to understand what it means. Then it takes that knowledge and outputs low-level instructions that produce the same semantics. Many languages split those two roles into two separate passes in the implementation. A parser produces an AST—just like jlox does—and then a code generator traverses the AST and outputs target code.

In clox, we’re taking an old-school approach and merging these two passes into one. Back in the day, language hackers did this because computers literally didn’t have enough memory to store an entire source file’s AST. We’re doing it because it keeps our compiler simpler, which is a real asset when programming in C.

Single-pass compilers like we’re going to build don’t work well for all languages. Since the compiler has only a peephole view into the user’s program while generating code, the language must be designed such that you don’t need much surrounding context to understand a piece of syntax. Fortunately, tiny, dynamically typed Lox is well-suited to that.

What this means in practical terms is that our “compiler” C module has functionality you’ll recognize from jlox for parsing—consuming tokens, matching expected token types, etc. And it also has functions for code gen—emitting bytecode and adding constants to the destination chunk. (And it means I’ll use “parsing” and “compiling” interchangeably throughout this and later chapters.)

We’ll build the parsing and code generation halves first. Then we’ll stitch them together with the code in the middle that uses Pratt’s technique to parse Lox’s particular grammar and output the right bytecode.

17 . 2Parsing Tokens

First up, the front half of the compiler. This function’s name should sound familiar.

#include "scanner.h"

static void advance() {
  parser.previous = parser.current;

  for (;;) {
    parser.current = scanToken();
    if (parser.current.type != TOKEN_ERROR) break;

    errorAtCurrent(parser.current.start);
  }
}

Just like in jlox, it steps forward through the token stream. It asks the scanner for the next token and stores it for later use. Before doing that, it takes the old current token and stashes that in a previous field. That will come in handy later so that we can get at the lexeme after we match a token.

The code to read the next token is wrapped in a loop. Remember, clox’s scanner doesn’t report lexical errors. Instead, it creates special error tokens and leaves it up to the parser to report them. We do that here.

We keep looping, reading tokens and reporting the errors, until we hit a non-error one or reach the end. That way, the rest of the parser sees only valid tokens. The current and previous token are stored in this struct:

#include "scanner.h"

typedef struct {
  Token current;
  Token previous;
} Parser;

Parser parser;

static void advance() {

Like we did in other modules, we have a single global variable of this struct type so we don’t need to pass the state around from function to function in the compiler.

17 . 2 . 1Handling syntax errors

If the scanner hands us an error token, we need to actually tell the user. That happens using this:

static void errorAtCurrent(const char* message) {
  errorAt(&parser.current, message);
}

We pull the location out of the current token in order to tell the user where the error occurred and forward it to errorAt(). More often, we’ll report an error at the location of the token we just consumed, so we give the shorter name to this other function:

static void error(const char* message) {
  errorAt(&parser.previous, message);
}

The actual work happens here:

static void errorAt(Token* token, const char* message) {
  fprintf(stderr, "[line %d] Error", token->line);

  if (token->type == TOKEN_EOF) {
    fprintf(stderr, " at end");
  } else if (token->type == TOKEN_ERROR) {
    // Nothing.
  } else {
    fprintf(stderr, " at '%.*s'", token->length, token->start);
  }

  fprintf(stderr, ": %s\n", message);
  parser.hadError = true;
}

First, we print where the error occurred. We try to show the lexeme if it’s human-readable. Then we print the error message itself. After that, we set this hadError flag. That records whether any errors occurred during compilation. This field also lives in the parser struct.

  Token previous;

  bool hadError;

} Parser;

Earlier I said that compile() should return false if an error occurred. Now we can make it do that.

  consume(TOKEN_EOF, "Expect end of expression.");

  return !parser.hadError;

}

I’ve got another flag to introduce for error handling. We want to avoid error cascades. If the user has a mistake in their code and the parser gets confused about where it is in the grammar, we don’t want it to spew out a whole pile of meaningless knock-on errors after the first one.

We fixed that in jlox using panic mode error recovery. In the Java interpreter, we threw an exception to unwind out of all of the parser code to a point where we could skip tokens and resynchronize. We don’t have exceptions in C. Instead, we’ll do a little smoke and mirrors. We add a flag to track whether we’re currently in panic mode.

  bool hadError;

  bool panicMode;

} Parser;

When an error occurs, we set it.

static void errorAt(Token* token, const char* message) {

  parser.panicMode = true;

  fprintf(stderr, "[line %d] Error", token->line);

After that, we go ahead and keep compiling as normal as if the error never occurred. The bytecode will never get executed, so it’s harmless to keep on trucking. The trick is that while the panic mode flag is set, we simply suppress any other errors that get detected.

static void errorAt(Token* token, const char* message) {

  if (parser.panicMode) return;

  parser.panicMode = true;

There’s a good chance the parser will go off in the weeds, but the user won’t know because the errors all get swallowed. Panic mode ends when the parser reaches a synchronization point. For Lox, we chose statement boundaries, so when we later add those to our compiler, we’ll clear the flag there.

These new fields need to be initialized.

  initScanner(source);

  parser.hadError = false;
  parser.panicMode = false;

  advance();

And to display the errors, we need a standard header.

#include <stdio.h>

#include <stdlib.h>

#include "common.h"

There’s one last parsing function, another old friend from jlox.

static void consume(TokenType type, const char* message) {
  if (parser.current.type == type) {
    advance();
    return;
  }

  errorAtCurrent(message);
}

It’s similar to advance() in that it reads the next token. But it also validates that the token has an expected type. If not, it reports an error. This function is the foundation of most syntax errors in the compiler.

OK, that’s enough on the front end for now.

17 . 3Emitting Bytecode

After we parse and understand a piece of the user’s program, the next step is to translate that to a series of bytecode instructions. It starts with the easiest possible step: appending a single byte to the chunk.

static void emitByte(uint8_t byte) {
  writeChunk(currentChunk(), byte, parser.previous.line);
}

It’s hard to believe great things will flow through such a simple function. It writes the given byte, which may be an opcode or an operand to an instruction. It sends in the previous token’s line information so that runtime errors are associated with that line.

The chunk that we’re writing gets passed into compile(), but it needs to make its way to emitByte(). To do that, we rely on this intermediary function:

Parser parser;

Chunk* compilingChunk;

static Chunk* currentChunk() {
  return compilingChunk;
}

static void errorAt(Token* token, const char* message) {

Right now, the chunk pointer is stored in a module-level variable like we store other global state. Later, when we start compiling user-defined functions, the notion of “current chunk” gets more complicated. To avoid having to go back and change a lot of code, I encapsulate that logic in the currentChunk() function.

We initialize this new module variable before we write any bytecode:

bool compile(const char* source, Chunk* chunk) {
  initScanner(source);

  compilingChunk = chunk;

  parser.hadError = false;

Then, at the very end, when we’re done compiling the chunk, we wrap things up.

  consume(TOKEN_EOF, "Expect end of expression.");

  endCompiler();

  return !parser.hadError;

That calls this:

static void endCompiler() {
  emitReturn();
}

In this chapter, our VM deals only with expressions. When you run clox, it will parse, compile, and execute a single expression, then print the result. To print that value, we are temporarily using the OP_RETURN instruction. So we have the compiler add one of those to the end of the chunk.

static void emitReturn() {
  emitByte(OP_RETURN);
}

While we’re here in the back end we may as well make our lives easier.

static void emitBytes(uint8_t byte1, uint8_t byte2) {
  emitByte(byte1);
  emitByte(byte2);
}

Over time, we’ll have enough cases where we need to write an opcode followed by a one-byte operand that it’s worth defining this convenience function.

17 . 4Parsing Prefix Expressions

We’ve assembled our parsing and code generation utility functions. The missing piece is the code in the middle that connects those together.

The only step in compile() that we have left to implement is this function:

static void expression() {
  // What goes here?
}

We aren’t ready to implement every kind of expression in Lox yet. Heck, we don’t even have Booleans. For this chapter, we’re only going to worry about four:

• Number literals: 123
• Parentheses for grouping: (123)
• Unary negation: -123
• The Four Horsemen of the Arithmetic: +, -, *, /

As we work through the functions to compile each of those kinds of expressions, we’ll also assemble the requirements for the table-driven parser that calls them.

17 . 4 . 1Parsers for tokens

For now, let’s focus on the Lox expressions that are each only a single token. In this chapter, that’s just number literals, but there will be more later. Here’s how we can compile them:

We map each token type to a different kind of expression. We define a function for each expression that outputs the appropriate bytecode. Then we build an array of function pointers. The indexes in the array correspond to the TokenType enum values, and the function at each index is the code to compile an expression of that token type.

To compile number literals, we store a pointer to the following function at the TOKEN_NUMBER index in the array.

static void number() {
  double value = strtod(parser.previous.start, NULL);
  emitConstant(value);
}

We assume the token for the number literal has already been consumed and is stored in previous. We take that lexeme and use the C standard library to convert it to a double value. Then we generate the code to load that value using this function:

static void emitConstant(Value value) {
  emitBytes(OP_CONSTANT, makeConstant(value));
}

First, we add the value to the constant table, then we emit an OP_CONSTANT instruction that pushes it onto the stack at runtime. To insert an entry in the constant table, we rely on:

static uint8_t makeConstant(Value value) {
  int constant = addConstant(currentChunk(), value);
  if (constant > UINT8_MAX) {
    error("Too many constants in one chunk.");
    return 0;
  }

  return (uint8_t)constant;
}

Most of the work happens in addConstant(), which we defined back in an earlier chapter. That adds the given value to the end of the chunk’s constant table and returns its index. The new function’s job is mostly to make sure we don’t have too many constants. Since the OP_CONSTANT instruction uses a single byte for the index operand, we can store and load only up to 256 constants in a chunk.

That’s basically all it takes. Provided there is some suitable code that consumes a TOKEN_NUMBER token, looks up number() in the function pointer array, and then calls it, we can now compile number literals to bytecode.

17 . 4 . 2Parentheses for grouping

Our as-yet-imaginary array of parsing function pointers would be great if every expression was only a single token long. Alas, most are longer. However, many expressions start with a particular token. We call these prefix expressions. For example, when we’re parsing an expression and the current token is (, we know we must be looking at a parenthesized grouping expression.

It turns out our function pointer array handles those too. The parsing function for an expression type can consume any additional tokens that it wants to, just like in a regular recursive descent parser. Here’s how parentheses work:

static void grouping() {
  expression();
  consume(TOKEN_RIGHT_PAREN, "Expect ')' after expression.");
}

Again, we assume the initial ( has already been consumed. We recursively call back into expression() to compile the expression between the parentheses, then parse the closing ) at the end.

As far as the back end is concerned, there’s literally nothing to a grouping expression. Its sole function is syntactic—it lets you insert a lower-precedence expression where a higher precedence is expected. Thus, it has no runtime semantics on its own and therefore doesn’t emit any bytecode. The inner call to expression() takes care of generating bytecode for the expression inside the parentheses.

17 . 4 . 3Unary negation

Unary minus is also a prefix expression, so it works with our model too.

static void unary() {
  TokenType operatorType = parser.previous.type;

  // Compile the operand.
  expression();

  // Emit the operator instruction.
  switch (operatorType) {
    case TOKEN_MINUS: emitByte(OP_NEGATE); break;
    default: return; // Unreachable.
  }
}

The leading - token has been consumed and is sitting in parser.previous. We grab the token type from that to note which unary operator we’re dealing with. It’s unnecessary right now, but this will make more sense when we use this same function to compile the ! operator in the next chapter.

As in grouping(), we recursively call expression() to compile the operand. After that, we emit the bytecode to perform the negation. It might seem a little weird to write the negate instruction after its operand’s bytecode since the - appears on the left, but think about it in terms of order of execution:

1. We evaluate the operand first which leaves its value on the stack.

2. Then we pop that value, negate it, and push the result.

So the OP_NEGATE instruction should be emitted last. This is part of the compiler’s job—parsing the program in the order it appears in the source code and rearranging it into the order that execution happens.

There is one problem with this code, though. The expression() function it calls will parse any expression for the operand, regardless of precedence. Once we add binary operators and other syntax, that will do the wrong thing. Consider:

-a.b + c;

Here, the operand to - should be just the a.b expression, not the entire a.b + c. But if unary() calls expression(), the latter will happily chew through all of the remaining code including the +. It will erroneously treat the - as lower precedence than the +.

When parsing the operand to unary -, we need to compile only expressions at a certain precedence level or higher. In jlox’s recursive descent parser we accomplished that by calling into the parsing method for the lowest-precedence expression we wanted to allow (in this case, call()). Each method for parsing a specific expression also parsed any expressions of higher precedence too, so that included the rest of the precedence table.

The parsing functions like number() and unary() here in clox are different. Each only parses exactly one type of expression. They don’t cascade to include higher-precedence expression types too. We need a different solution, and it looks like this:

static void parsePrecedence(Precedence precedence) {
  // What goes here?
}

This function—once we implement it—starts at the current token and parses any expression at the given precedence level or higher. We have some other setup to get through before we can write the body of this function, but you can probably guess that it will use that table of parsing function pointers I’ve been talking about. For now, don’t worry too much about how it works. In order to take the “precedence” as a parameter, we define it numerically.

} Parser;

typedef enum {
  PREC_NONE,
  PREC_ASSIGNMENT,  // =
  PREC_OR,          // or
  PREC_AND,         // and
  PREC_EQUALITY,    // == !=
  PREC_COMPARISON,  // < > <= >=
  PREC_TERM,        // + -
  PREC_FACTOR,      // * /
  PREC_UNARY,       // ! -
  PREC_CALL,        // . ()
  PREC_PRIMARY
} Precedence;

Parser parser;

These are all of Lox’s precedence levels in order from lowest to highest. Since C implicitly gives successively larger numbers for enums, this means that PREC_CALL is numerically larger than PREC_UNARY. For example, say the compiler is sitting on a chunk of code like:

-a.b + c

If we call parsePrecedence(PREC_ASSIGNMENT), then it will parse the entire expression because + has higher precedence than assignment. If instead we call parsePrecedence(PREC_UNARY), it will compile the -a.b and stop there. It doesn’t keep going through the + because the addition has lower precedence than unary operators.

With this function in hand, it’s a snap to fill in the missing body for expression().

static void expression() {

  parsePrecedence(PREC_ASSIGNMENT);

}

We simply parse the lowest precedence level, which subsumes all of the higher-precedence expressions too. Now, to compile the operand for a unary expression, we call this new function and limit it to the appropriate level:

  // Compile the operand.

  parsePrecedence(PREC_UNARY);

  // Emit the operator instruction.

We use the unary operator’s own PREC_UNARY precedence to permit nested unary expressions like !!doubleNegative. Since unary operators have pretty high precedence, that correctly excludes things like binary operators. Speaking of which . . . 

17 . 5Parsing Infix Expressions

Binary operators are different from the previous expressions because they are infix. With the other expressions, we know what we are parsing from the very first token. With infix expressions, we don’t know we’re in the middle of a binary operator until after we’ve parsed its left operand and then stumbled onto the operator token in the middle.

Here’s an example:

1 + 2

Let’s walk through trying to compile it with what we know so far:

1. We call expression(). That in turn calls parsePrecedence(PREC_ASSIGNMENT).

2. That function (once we implement it) sees the leading number token and recognizes it is parsing a number literal. It hands off control to number().

3. number() creates a constant, emits an OP_CONSTANT, and returns back to parsePrecedence().

Now what? The call to parsePrecedence() should consume the entire addition expression, so it needs to keep going somehow. Fortunately, the parser is right where we need it to be. Now that we’ve compiled the leading number expression, the next token is +. That’s the exact token that parsePrecedence() needs to detect that we’re in the middle of an infix expression and to realize that the expression we already compiled is actually an operand to that.

So this hypothetical array of function pointers doesn’t just list functions to parse expressions that start with a given token. Instead, it’s a table of function pointers. One column associates prefix parser functions with token types. The second column associates infix parser functions with token types.

The function we will use as the infix parser for TOKEN_PLUS, TOKEN_MINUS, TOKEN_STAR, and TOKEN_SLASH is this:

static void binary() {
  TokenType operatorType = parser.previous.type;
  ParseRule* rule = getRule(operatorType);
  parsePrecedence((Precedence)(rule->precedence + 1));

  switch (operatorType) {
    case TOKEN_PLUS:          emitByte(OP_ADD); break;
    case TOKEN_MINUS:         emitByte(OP_SUBTRACT); break;
    case TOKEN_STAR:          emitByte(OP_MULTIPLY); break;
    case TOKEN_SLASH:         emitByte(OP_DIVIDE); break;
    default: return; // Unreachable.
  }
}

When a prefix parser function is called, the leading token has already been consumed. An infix parser function is even more in medias res—the entire left-hand operand expression has already been compiled and the subsequent infix operator consumed.

The fact that the left operand gets compiled first works out fine. It means at runtime, that code gets executed first. When it runs, the value it produces will end up on the stack. That’s right where the infix operator is going to need it.

Then we come here to binary() to handle the rest of the arithmetic operators. This function compiles the right operand, much like how unary() compiles its own trailing operand. Finally, it emits the bytecode instruction that performs the binary operation.

When run, the VM will execute the left and right operand code, in that order, leaving their values on the stack. Then it executes the instruction for the operator. That pops the two values, computes the operation, and pushes the result.

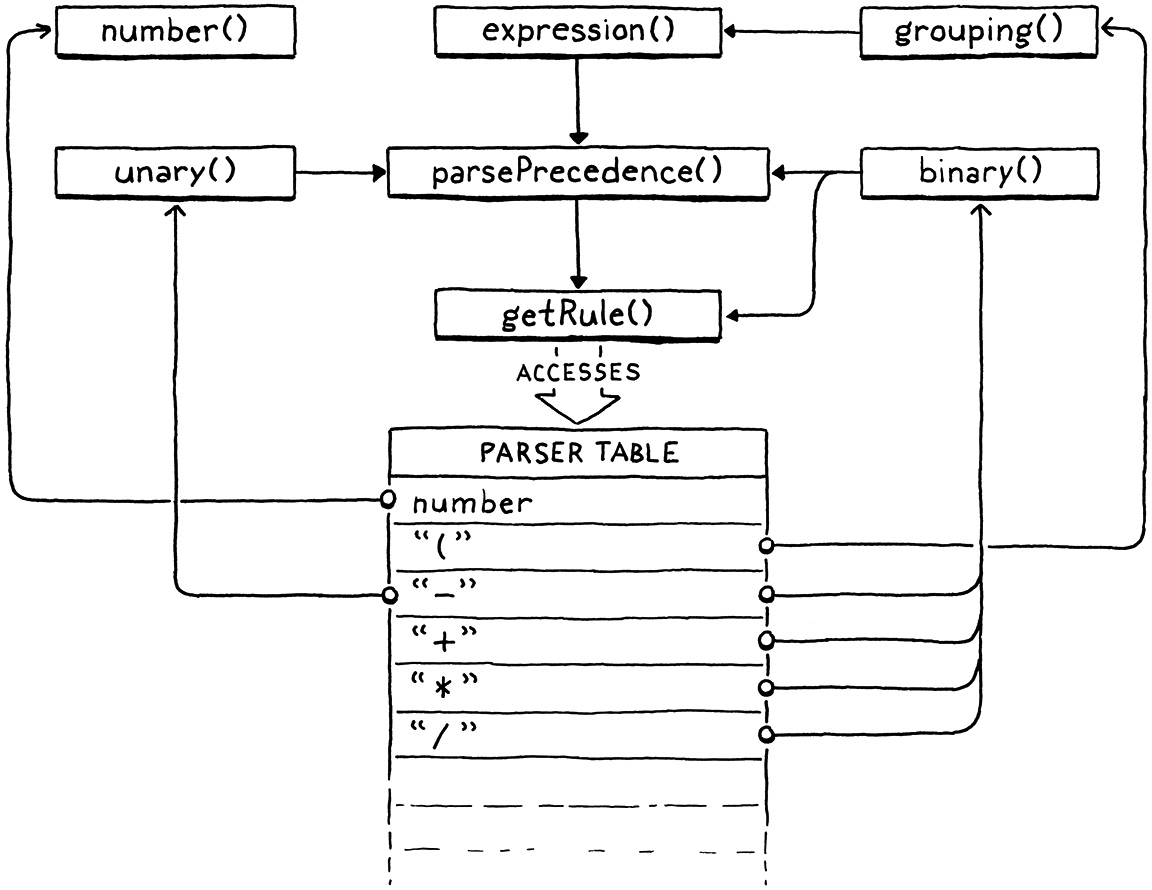
The code that probably caught your eye here is that getRule() line. When we parse the right-hand operand, we again need to worry about precedence. Take an expression like:

2 * 3 + 4

When we parse the right operand of the * expression, we need to just capture 3, and not 3 + 4, because + is lower precedence than *. We could define a separate function for each binary operator. Each would call parsePrecedence() and pass in the correct precedence level for its operand.

But that’s kind of tedious. Each binary operator’s right-hand operand precedence is one level higher than its own. We can look that up dynamically with this getRule() thing we’ll get to soon. Using that, we call parsePrecedence() with one level higher than this operator’s level.

This way, we can use a single binary() function for all binary operators even though they have different precedences.

17 . 6A Pratt Parser

We now have all of the pieces and parts of the compiler laid out. We have a function for each grammar production: number(), grouping(), unary(), and binary(). We still need to implement parsePrecedence(), and getRule(). We also know we need a table that, given a token type, lets us find

• the function to compile a prefix expression starting with a token of that type,

• the function to compile an infix expression whose left operand is followed by a token of that type, and

• the precedence of an infix expression that uses that token as an operator.

We wrap these three properties in a little struct which represents a single row in the parser table.

} Precedence;

typedef struct {
  ParseFn prefix;
  ParseFn infix;
  Precedence precedence;
} ParseRule;

Parser parser;

That ParseFn type is a simple typedef for a function type that takes no arguments and returns nothing.

} Precedence;

typedef void (*ParseFn)();

typedef struct {

The table that drives our whole parser is an array of ParseRules. We’ve been talking about it forever, and finally you get to see it.

ParseRule rules[] = {
  [TOKEN_LEFT_PAREN]    = {grouping, NULL,   PREC_NONE},
  [TOKEN_RIGHT_PAREN]   = {NULL,     NULL,   PREC_NONE},
  [TOKEN_LEFT_BRACE]    = {NULL,     NULL,   PREC_NONE}, 
  [TOKEN_RIGHT_BRACE]   = {NULL,     NULL,   PREC_NONE},
  [TOKEN_COMMA]         = {NULL,     NULL,   PREC_NONE},
  [TOKEN_DOT]           = {NULL,     NULL,   PREC_NONE},
  [TOKEN_MINUS]         = {unary,    binary, PREC_TERM},
  [TOKEN_PLUS]          = {NULL,     binary, PREC_TERM},
  [TOKEN_SEMICOLON]     = {NULL,     NULL,   PREC_NONE},
  [TOKEN_SLASH]         = {NULL,     binary, PREC_FACTOR},
  [TOKEN_STAR]          = {NULL,     binary, PREC_FACTOR},
  [TOKEN_BANG]          = {NULL,     NULL,   PREC_NONE},
  [TOKEN_BANG_EQUAL]    = {NULL,     NULL,   PREC_NONE},
  [TOKEN_EQUAL]         = {NULL,     NULL,   PREC_NONE},
  [TOKEN_EQUAL_EQUAL]   = {NULL,     NULL,   PREC_NONE},
  [TOKEN_GREATER]       = {NULL,     NULL,   PREC_NONE},
  [TOKEN_GREATER_EQUAL] = {NULL,     NULL,   PREC_NONE},
  [TOKEN_LESS]          = {NULL,     NULL,   PREC_NONE},
  [TOKEN_LESS_EQUAL]    = {NULL,     NULL,   PREC_NONE},
  [TOKEN_IDENTIFIER]    = {NULL,     NULL,   PREC_NONE},
  [TOKEN_STRING]        = {NULL,     NULL,   PREC_NONE},
  [TOKEN_NUMBER]        = {number,   NULL,   PREC_NONE},
  [TOKEN_AND]           = {NULL,     NULL,   PREC_NONE},
  [TOKEN_CLASS]         = {NULL,     NULL,   PREC_NONE},
  [TOKEN_ELSE]          = {NULL,     NULL,   PREC_NONE},
  [TOKEN_FALSE]         = {NULL,     NULL,   PREC_NONE},
  [TOKEN_FOR]           = {NULL,     NULL,   PREC_NONE},
  [TOKEN_FUN]           = {NULL,     NULL,   PREC_NONE},
  [TOKEN_IF]            = {NULL,     NULL,   PREC_NONE},
  [TOKEN_NIL]           = {NULL,     NULL,   PREC_NONE},
  [TOKEN_OR]            = {NULL,     NULL,   PREC_NONE},
  [TOKEN_PRINT]         = {NULL,     NULL,   PREC_NONE},
  [TOKEN_RETURN]        = {NULL,     NULL,   PREC_NONE},
  [TOKEN_SUPER]         = {NULL,     NULL,   PREC_NONE},
  [TOKEN_THIS]          = {NULL,     NULL,   PREC_NONE},
  [TOKEN_TRUE]          = {NULL,     NULL,   PREC_NONE},
  [TOKEN_VAR]           = {NULL,     NULL,   PREC_NONE},
  [TOKEN_WHILE]         = {NULL,     NULL,   PREC_NONE},
  [TOKEN_ERROR]         = {NULL,     NULL,   PREC_NONE},
  [TOKEN_EOF]           = {NULL,     NULL,   PREC_NONE},
};

You can see how grouping and unary are slotted into the prefix parser column for their respective token types. In the next column, binary is wired up to the four arithmetic infix operators. Those infix operators also have their precedences set in the last column.

Aside from those, the rest of the table is full of NULL and PREC_NONE. Most of those empty cells are because there is no expression associated with those tokens. You can’t start an expression with, say, else, and } would make for a pretty confusing infix operator.

But, also, we haven’t filled in the entire grammar yet. In later chapters, as we add new expression types, some of these slots will get functions in them. One of the things I like about this approach to parsing is that it makes it very easy to see which tokens are in use by the grammar and which are available.

Now that we have the table, we are finally ready to write the code that uses it. This is where our Pratt parser comes to life. The easiest function to define is getRule().

static ParseRule* getRule(TokenType type) {
  return &rules[type];
}

It simply returns the rule at the given index. It’s called by binary() to look up the precedence of the current operator. This function exists solely to handle a declaration cycle in the C code. binary() is defined before the rules table so that the table can store a pointer to it. That means the body of binary() cannot access the table directly.

Instead, we wrap the lookup in a function. That lets us forward declare getRule() before the definition of binary(), and then define getRule() after the table. We’ll need a couple of other forward declarations to handle the fact that our grammar is recursive, so let’s get them all out of the way.

  emitReturn();
}

static void expression();
static ParseRule* getRule(TokenType type);
static void parsePrecedence(Precedence precedence);

static void binary() {

If you’re following along and implementing clox yourself, pay close attention to the little annotations that tell you where to put these code snippets. Don’t worry, though, if you get it wrong, the C compiler will be happy to tell you.

17 . 6 . 1Parsing with precedence

Now we’re getting to the fun stuff. The maestro that orchestrates all of the parsing functions we’ve defined is parsePrecedence(). Let’s start with parsing prefix expressions.

static void parsePrecedence(Precedence precedence) {

  advance();
  ParseFn prefixRule = getRule(parser.previous.type)->prefix;
  if (prefixRule == NULL) {
    error("Expect expression.");
    return;
  }

  prefixRule();

}

We read the next token and look up the corresponding ParseRule. If there is no prefix parser, then the token must be a syntax error. We report that and return to the caller.

Otherwise, we call that prefix parse function and let it do its thing. That prefix parser compiles the rest of the prefix expression, consuming any other tokens it needs, and returns back here. Infix expressions are where it gets interesting since precedence comes into play. The implementation is remarkably simple.

  prefixRule();

  while (precedence <= getRule(parser.current.type)->precedence) {
    advance();
    ParseFn infixRule = getRule(parser.previous.type)->infix;
    infixRule();
  }

}

That’s the whole thing. Really. Here’s how the entire function works: At the beginning of parsePrecedence(), we look up a prefix parser for the current token. The first token is always going to belong to some kind of prefix expression, by definition. It may turn out to be nested as an operand inside one or more infix expressions, but as you read the code from left to right, the first token you hit always belongs to a prefix expression.

After parsing that, which may consume more tokens, the prefix expression is done. Now we look for an infix parser for the next token. If we find one, it means the prefix expression we already compiled might be an operand for it. But only if the call to parsePrecedence() has a precedence that is low enough to permit that infix operator.

If the next token is too low precedence, or isn’t an infix operator at all, we’re done. We’ve parsed as much expression as we can. Otherwise, we consume the operator and hand off control to the infix parser we found. It consumes whatever other tokens it needs (usually the right operand) and returns back to parsePrecedence(). Then we loop back around and see if the next token is also a valid infix operator that can take the entire preceding expression as its operand. We keep looping like that, crunching through infix operators and their operands until we hit a token that isn’t an infix operator or is too low precedence and stop.

That’s a lot of prose, but if you really want to mind meld with Vaughan Pratt and fully understand the algorithm, step through the parser in your debugger as it works through some expressions. Maybe a picture will help. There’s only a handful of functions, but they are marvelously intertwined:

Later, we’ll need to tweak the code in this chapter to handle assignment. But, otherwise, what we wrote covers all of our expression compiling needs for the rest of the book. We’ll plug additional parsing functions into the table when we add new kinds of expressions, but parsePrecedence() is complete.

17 . 7Dumping Chunks

While we’re here in the core of our compiler, we should put in some instrumentation. To help debug the generated bytecode, we’ll add support for dumping the chunk once the compiler finishes. We had some temporary logging earlier when we hand-authored the chunk. Now we’ll put in some real code so that we can enable it whenever we want.

Since this isn’t for end users, we hide it behind a flag.

#include <stdint.h>

#define DEBUG_PRINT_CODE

#define DEBUG_TRACE_EXECUTION

When that flag is defined, we use our existing “debug” module to print out the chunk’s bytecode.

  emitReturn();

#ifdef DEBUG_PRINT_CODE
  if (!parser.hadError) {
    disassembleChunk(currentChunk(), "code");
  }
#endif

}

We do this only if the code was free of errors. After a syntax error, the compiler keeps on going but it’s in kind of a weird state and might produce broken code. That’s harmless because it won’t get executed, but we’ll just confuse ourselves if we try to read it.

Finally, to access disassembleChunk(), we need to include its header.

#include "scanner.h"

#ifdef DEBUG_PRINT_CODE
#include "debug.h"
#endif

typedef struct {

We made it! This was the last major section to install in our VM’s compilation and execution pipeline. Our interpreter doesn’t look like much, but inside it is scanning, parsing, compiling to bytecode, and executing.

Fire up the VM and type in an expression. If we did everything right, it should calculate and print the result. We now have a very over-engineered arithmetic calculator. We have a lot of language features to add in the coming chapters, but the foundation is in place.